И все-таки, Гранди! - математическая смекалка

1. Двое играют в следующую странную, о чем позднее, игру:

- у них есть кучка камней, причем камней нечетное число;

- они берут по-очереди камни из кучки, причем не более четырех за раз;

- так продолжается, пока всю кучку не разберут, и тогда победил тот, кто взял четное число камней.

На первый взгляд, игра не поддается анализу с помощью функции Гранди:

1. Состояние кучки не определяет положение в игре, т.к. важны еще камни игроков.

Но это легко устраняется, берем в качестве состояния игры тройку:

(n, m, p),

где n - число камней в кучке,

m - четность числа камней у игрока, чей ход,

p - четность числа камней у другого игрока.

В дальнейшем 0 - означает четное, а 1 - нечетное число камней.

Такое определение состояния игры восстанавливает симметрию между игроками, но возникает следующее затруднение:

2. Игра заканчивается, когда камней в куче нет, т.е. n=0. Но таких позиций у нас две (вспоминаем, что общее число камней нечетно):

(0,1,0)         [1]

(0,0,1)         [2]

Если позиция [1] удовлетворяет нашим понятиям о конце игры: хода нет, у игрока, который должен ходить, нечетное число камней, и он, следовательно, проиграл, то позиция [2] несколько странна: хода нет, но ходящий из нее не проиграл (!), ведь у него четное число камней...

Устраняем эту странность формально - считаем, что в позиции [2] начинающий может сделать пустой ход, переводя ее в позицию [1]. Т.е. на графе игры добавляем дугу:

(0,0,1) --> (0,1,0)

Теперь строим функцию Гранди, для чего рисуем кусок графа игры. Из каждой вершины выходят не более четырех дуг.

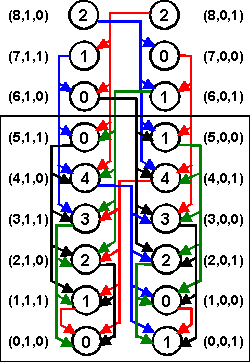
Рис. 1

Можно заметить разного рода симметрию этого графа, но это лирика... Определяем функцию Гранди на вершинах стандартным образом:

Gr((0,1,0))=0

Gr(x)=min(N0 \ {Gr(t) | t in Gx}),

где Gr(x) - значение функции Гранди в вершине x,

N0 - множество неотрицательных целых чисел,

Gx - множество концов дуг с началом в вершине x, или, это множество позиций, в которые можно перейти, сделав ход в позиции x.

Результат вычислений показан на том же рис. 1. - значения функции Гранди даны в кружках. Функция оказывается периодической с периодом длины 6, который обведен на рис. 1. тонким прямоугольником. Желающие могут сами доказать периодичность, а мы перейдем к формулам.

Периодичность означает следующее:

Gr((n,m,p))=Gr((a,m,p)),

где n=a (mod 6).

Так как в начале игры камней на руках нет, а в кучке нечетное число, то позиция имеет вид:

(n,0,0),

где n - нечетное.

Получаем соотношения:

Gr((n,0,0))=1, при n=5 (mod 6)

Gr((n,0,0))=3, при n=3 (mod 6)

Gr((n,0,0))=0, при n=1 (mod 6)

Кстати, в задаче 286 Кордемского n=27, т.е.

Gr((27,0,0))=Gr((3,0,0))=3,

начинающий выигрывает, и ход, переводящий игру в нулевую позицию, можно увидеть из графа - он эквивалентен ходу

(3,0,0) --> (1,0,0),

т.е. начинающий берет два камня.

Я в начале обмолвился о странности этой игры, но представим себе такой вариант: в куче есть протоны и электроны, выигрывает тот, у кого заряд меньше по модулю, т.е. ближе к нулю. А если еще добавить нейтроны,.. то можно вообразить себя богом-творцом.

По материалам задачи 286 из книги Кордемского "Математическая смекалка", издание 10-е, МДС, 1994

Автор Алексей ТЕТЕРКО (Черкассы)