Шур А.Б. Мои отношения с математикой
Posted by Pretich on December 06 2023 12:13:44
О том, как я учился и учил математике - Шур Александр Борисович
Часть 1 - Часть 2
Необходимое пояснение
 Такой раздел может показаться странным при моей профессии. Но большинство моих металлургических забот, так или иначе, были связаны с математикой, особенно после появления ЭВМ, когда реальностью стали математические модели металлургических процессов. Приходилось многое осваивать самому – вузовского багажа не хватало: составители учебных программ считали, что металлургам математика не особо нужна.
Такой раздел может показаться странным при моей профессии. Но большинство моих металлургических забот, так или иначе, были связаны с математикой, особенно после появления ЭВМ, когда реальностью стали математические модели металлургических процессов. Приходилось многое осваивать самому – вузовского багажа не хватало: составители учебных программ считали, что металлургам математика не особо нужна.
Когда сам стал преподавать, пришлось реанимировать математические знания и умения у студентов, якобы обученных математике, а на самом деле воспитанных в стойком отвращении к ней.
Этот опыт убедил меня в том, что вузовское и школьное математическое образование имеет изъяны. Цели, отбор материала, расстановка акцентов, методики изложения – все требует пересмотра. Кроме критики, пришлось заняться конкретными методическими разработками.
Итак, студенческие воспоминания, математические модели и проблемы учебного процесса.
Начало
В детстве и юности я математикой интересовался “бескорыстно”, не задумываясь над тем, где и когда она мне понадобится для дела. Теоретически я, конечно, понимал, что она нужна для технических расчетов. Практически же, если не считать задач, не более сложных, чем расчеты у кассы в магазине, эти две сферы – математика и инженерная практика – существовали как бы в разных мирах.
Но вот однажды мне, студенту 1 курса, попала на один вечер в руки книга: Г.М. Фихтенгольц, Математика для инженеров. Книга эта совершила буквально переворот в моих представлениях – может быть, не столько в сознании, сколько в подсознании. И решающим, как ни странно, оказался совсем простой пример – эллиптическая зубчатая передача. Тот факт, что сумма расстояний от любой точки эллипса до его фокусов есть постоянная величина, равная его большой оси, мне был, конечно, хорошо известен, но никаких эмоций не вызывал. И вдруг – столь реальное практическое воплощение. Если поместить валы в фокусах двух одинаковых эллиптических зубчатых колес и разнести их на расстояние, равное большой оси, эти шестеренки будут все время находиться в зацеплении, и равномерно вращая ведущую, получаем переменную скорость вращения ведомой. Помню первое впечатление: этого не может быть! Но логика сильнее эмоций (к сожалению, не всегда).
Самой этой идеей мне никогда воспользоваться не пришлось. Но она дала определенный толчок направлению мыслей, и не только потому, что математика соединилась с жизнью. Важно было оценить и то, чем этот толчок был вызван, и понять, что хороший наглядный пример бывает полезнее иных многословных рассуждений. В том числе и для формирования мировоззрения. Это очень помогало мне впоследствии, особенно, когда сам стал преподавать.
Вездесущий Зельдович
Имя Я.Б. Зельдовича мне было известно давно – ведь он один из тех, кто заложил основы металлургической кинетики. (Одно время я даже считал металлургию главным кругом его интересов. Эта ошибка объяснима – он был сильно засекреченной фигурой, о чем я узнал впоследствии из воспоминаний А.Д. Сахарова). Потом его фамилия мелькала в статьях и книгах по астрофизике и другим экзотическим проблемам.
Когда я увидел его книгу “Высшая математика для начинающих”, то вначале удивился, а потом понял: это – то, чего так не хватало. И каков диапазон творческих достижений! Химическая кинетика, горение и взрыв, атомная и термоядерная бомба, астрофизика, элементарные частицы, многое другое, и вот вдруг учебное пособие по математике, да еще и для начинающих. (Кстати, эту книгу высоко оценил и А.Д. Сахаров).
К тому времени я уже понял, что большинство учебников по математике для технических вузов написаны плохо. Нельзя будущего инженера учить этой науке так, как будущего математика, и дело не в объеме материала, а в самой направленности курса. Зельдович четко и ясно сказал то, что я смутно ощущал.
“Слишком много других учебников высшей математики ориентированы на читателя скептика и крючкотвора, который сопротивляется введению новых понятий, выдумывает возражения и исключения. От такого читателя приходится последовательно и упорно, с помощью строгой цепи теорем, логически следующих одна за другой, отбиваться.
Но лучше посоветовать скептику: сперва поверь на слово, пойми, о чем идет речь, где и как применяются производные и интегралы и все, о чем говорится в этой книге. После этого, став старше и образованнее, можешь вернуться к вопросу о строгости доказательств”.
Сама эта книга – пример того, каким должен быть учебник математики для физиков и инженеров. Могут сказать, что в ней многого недостает из предусмотренного программой. Но я убежден, что освоивший ее инженер будет на голову выше того, кто добросовестно “сдал” математику по действующим учебникам. Вот пример из преподавательского опыта. Студент 3 курса слабо усваивал мой предмет – теорию металлургических процессов. Беседуя с ним, я обнаружил, что он не понимает физической химии. Хотел начать с ее повторения, но выяснил, что все начинается с математики. Тогда посоветовал ему просто почитать книгу Зельдовича – как беллетристику, а если что будет неясно, то прийти с вопросами. Через несколько дней он прибежал в сильном возбуждении: “А.Б.! Да ведь я же наконец понял, чего они от меня хотели все эти годы!” (“они” – это преподаватели математики). После этого ему уже не понадобились никакие консультации ни по математике, ни по ФХ, ни по моему курсу. Он отлично сдал экзамен, а впоследствии успешно занимался научной работой. И пример этот не единственный. Жаль только, что книга превратилась в библиографическую редкость. Ее переиздание и пропагандирование дало бы для повышения успеваемости студентов больше, чем вся деятельность деканатов.
Добавление 2000 г. Подтверждая свою оценку книги, теперь я вижу и то, что кое в чем стоило бы пойти дальше, чем это сделал автор. Об этом несколько позже.
Для чего учить математике?
1. Математика – гимнастика для ума? Бесспорно. Но не только. Это еще и рабочий инструмент, а точнее – набор разнообразных инструментов. Но профессиональный снобизм математиков этим пренебрегает. Формы пренебрежения – разные. Головоломные задачи чаще всего проверяют изощренность ума, а в сочетании с не менее изощренным репетиторством – степень натасканности на всевозможные искусственные приемы. Это помогает сдать конкурсный экзамен, построенный по тем же правилам, но чаще всего уводит в сторону от того, что на самом деле требуется от математики в прикладных задачах.
Другая крайность (чем грешат спецкурсы) – приземленность прикладных расчетов – нередко ведет к механическому запоминанию определенного алгоритма без вникания в суть совершаемых действий, а заодно – без стремления его усовершенствовать и без умения выбрать нужный инструментарий из набора (или воспользоваться им) при возникновении новой задачи.
Если уж сравнивать со спортом, то (применительно к прикладным профессиям) лучше говорить о многоборье. А еще лучше сравнивать не с одним лишь спортом. Например, задачу – возможно быстрее попасть из пункта А в пункт Б – можно поставить самыми разными способами.
1) Можно проверить, кто попросту быстрее бежит.
2) Можно, как при спортивном ориентировании, бежать по лесу с картой и компасом.
3) Наконец, можно по лесистым горам искать дорогу без карты, зная лишь приблизительно направление (примеры помасштабнее – искать путь в Индию, как Колумб или Магеллан.
Всякая аналогия условна, но первый случай ближе к чистой математике, второй – к конструкторской работе, третий – к изобретательству или научным исследованиям. Кто возьмется сказать, что из них важнее? Математики учат своей науке так, как будто всех собираются сделать профессиональными математиками. Поставив (пусть и неосознанно) эту недостижимую цель, они не думают о других целях – достижимых и по настоящему нужных.
Можно и другое сказать. Даже инженеров разных специальностей желательно учить по-разному. Например, аналитическая геометрия в пространстве имеет прямое прикладное значение для горняков. Типичная задача: пробурив наклонный ствол, попасть в заданную точку подземного пространства. Ясно, что студент должен довести свои знания и умения по этому разделу до прочных навыков задолго до того, как столкнется с проблемами шахтостроения.
Напротив, для технологов – металлургов или химиков – этот раздел прямого практического выхода не имеет, а лишь полезен для других разделов математики. Зато для них необходим курс теории случайных процессов – к сожалению, не включенный в программы.
2. Есть очень простой тест, с которого я всегда начинаю проверку того, понимает ли человек математику. В декартовых координатах строится график функции – ломаная линия, состоящая из трех прямолинейных отрезков. Первый – крутой луч, идущий из начала координат (под углом 60-80°), второй продолжает его с меньшим наклоном (30-50°), третий – горизонтальный. Испытуемому предлагается под графиком построить (качественно, на глаз) график производной этой функции (чуть более сложный вариант – обратная задача: построить график определенного интеграла с переменным верхним пределом).
Когда я устроил такую проверку в первый раз, то пришел в ужас. Из 25 студентов считавшейся сильной группы 3 курса эту задачу сходу решили 2 или 3 человека. Еще 5-7 – после наводящего вопроса. Остальным потребовалась целая серия наводящих вопросов, а некоторым не хватило и этого. Впоследствии я стал относиться к этому спокойнее, хотя результаты с каждым годом становились хуже. (В двух “более солидных” вузах, где я читал гостевые лекции, сходу не решил никто, после наводящего вопроса – 2-3, после серии таких вопросов еще 4-5). Я понял, что это – неизбежный результат сложившейся системы образования (как среднего, так и высшего), и стал делать то, что в моих силах: латать дыры в прежней подготовке по общеобразовательным наукам (и не только математике). Не скажу, что это давало полный эффект. Но хотя бы несколько человек из группы удавалось убедить в том, что в любой науке главное – не “выучить”, а понять. Ведь чаще всего дело не в прямом незнании. C тестом не справлялись студенты, без запинки произносившие определение производной и даже умевшие продифференцировать функцию, заданную формулой. Многие и начинали с вопроса: “а где же формула?”. Слова и формулы никак не связывались с заложенным в них смыслом.
Возможно, кому-то покажется странным, но я это воспринимал как одно из проявлений бюрократизма. Бюрократизм со стороны преподавателя – добиваться формального знания. Со стороны начальников и контролеров всех уровней – выдавливать из преподавателя “процент”, и в то же время создавать видимость такого строгого контроля, при котором нельзя уйти от программ ни на шаг в сторону. Для самого студента – зародыш бюрократического подхода ко всему, к чему он потом прикоснется. Ведь что такое бюрократизм? Соблюдение формы при отсутствии интереса к сути дела. Цитируя вышедшего из моды классика, “По форме правильно, а по существу издевательство” – сначала над здравым смыслом, а потом над человеком.
3. Будучи одно время председателем методической комиссии факультета, я пытался воздействовать на этот процесс в самом его зародыше – то есть, в программах и методике преподавания математики. Но странное дело! От меня требовали совсем не этого, а “анализа учебного процесса”. Состоял он в том, что подсчитывались средний балл и “показатель качества” (доля повышенных оценок) и сравнивались по группам, преподавателям, с предыдущим семестром, и т.д., и делались глубокомысленные выводы о том, кто лучше, а кто хуже справляется с работой... В конечном счете, все сводилось к самому обыкновенному давлению на преподавателей, очковтирательству и выводиловке. Меня поражала способность десятков умных солидных людей часами на полном серьезе обсуждать (на совещаниях деканов, зав. кафедрами, общих собраниях) всю эту никчемную писанину. Мало того! Докладывать ее в Министерство, где ее тоже обсуждали... При этом любые попытки говорить по сути энергично пресекались.
4. Но вернусь к этой самой сути. Я долгое время настаивал на том, чтобы в курсе математики вначале изучали определенный интеграл, и лишь после этого – неопределенный. Кстати, именно так построена книга Зельдовича. Больше того, там и техника дифференцирования рассматривается после знакомства с определенным интегралом. Смысл этого – сделать упор на идейную сторону обоих понятий. Когда заведовать кафедрой математики в КГМИ стал М.В.Вишняков, он эту идею попытался осуществить (по собственной инициативе, независимо от моих пожеланий). Но продержался этот опыт недолго. Преподаватели никак не могли понять, что же они должны делать с этой идейной стороной и как вести упражнения. По моим наблюдениям, происходил ползучий возврат к старой схеме: “чтобы не терять времени”, пока на лекциях рассказывали о площадях под кривыми, на практических занятиях упражнялись в технике интегрирования, а для этого ассистенты кратенько рассказывали вместо лектора, что такое неопределенный интеграл, и получалось еще хуже, чем было до нововведения.
Поскольку я продолжаю считать, что лошадь должна быть впереди телеги, расскажу хотя бы здесь, какие – одновременно с этим – я проводил собственные упражнения со студентами группы металлургов, будучи ее куратором. Просьба к читателю-студенту: если Вы с листа не “видите”, о чем идет речь ниже – возьмите в руки лист бумаги в клетку и карандаш и рисуйте все подряд. Не пожалеете.
Итак, имеем на графике горизонтальную линию y=k, пересекающую ось ординат. Просьба определить площадь S прямоугольника, ограниченного слева осью ординат, снизу – осью абсцисс, сверху – нашей линией, и справа –вертикалью с абсциссой x. Правильно, S=k · x. (Задачка, конечно, для начальной школы, но я и добиваюсь, чтобы Вы на меня обиделись за недооценку ваших умственных способностей). А теперь под нашим графиком построим график этой площади, как функции переменной правой границы: S=f(x). Зависимость эта линейная, более того – прямо пропорциональная, и ее график – прямая, идущая из начала координат с угловым коэффициентом k. То, что мы построили – называется: определенный интеграл, как функция верхнего предела.
Решим теперь другую задачу: построить график производной функции S. Позвольте, но ведь она уже решена! Производная – это и есть угловой коэффициент, он для прямой везде постоянен и равен k, и искомый график – наша исходная горизонталь! Итак, Вы своими глазами убедились, что, по крайней мере, для прямых линий, интегрирование и дифференцирование (то есть, вычисление площадей и оценка крутизны линии) есть взаимно обратные действия.
Вернемся к исходной задаче. Нам теперь нужно определить площадь прямоугольника, ограниченного слева не осью ординат, а вертикалью с абсциссой a, правую же границу обозначим b. Напрашивается ответ S=(b–a) · k, но мы поступим иначе: выразим его как разность двух площадей – одна из них отсчитана от 0 до a, другая – от 0 до b: S = b · k – a · k. Простое раскрытие скобок? Нет, на самом деле мы вывели для простейшего случая формулу Ньютона-Лейбница. Для более сложных случаев такое примитивное доказательство не пройдет, но общая-то формула останется той же самой! А откуда она берется и что означает – лучше всего видно как раз здесь, на этом примитиве.
Продвинемся чуть дальше. Если строить графики S=f(x) для разных значений a, легко убедиться, что все они будут параллельны, пересекая горизонтальную ось каждая в своей точке a. График же производной для них всех будет один – все та же исходная горизонталь. Теперь можно усложнять и разнообразить задачу: менять уровень исходной горизонтали; брать в качестве исходной не горизонталь, а наклонную линию; ступенчатую, ломаную, и т.д.; начинать не с задачи интегрирования, а с дифференцирования, делать построение не “просто так”, а на бумаге в клетку с соблюдением масштабов, и т.д. Но я не собираясь превращать мемуар в методическое пособие, и на этом остановлюсь. Я хотел лишь показать, что и “без формул” есть что делать на упражнениях по интегрированию в рамках темы “определенный интеграл”, прочитанной в самом начале, сразу за введением понятия производной.
Не сомневаюсь в том, что любой штатный методист меня обвинит в примитивизации, может быть даже – в профанации курса математики. Ну что ж, я на это отвечу: подлинной профанацией не только математики, а и всего высшего образования вот уже много лет занимаются его руководители. А если кто в этом сомневается, пусть даст мои примитивные тесты любой группе хотя бы 3-го курса и посмотрит на результат. И это лишь верхушка айсберга.
5. Но вернусь к делу. Вот эти самые тесты – это и есть то самое, чего не хватало моим студентам для чтения программ, плотностей и функций распределения, эпюр моментов и перерезывающих сил. (Программа – спектр распределения поверхности пор по их радиусам).
Далее. Если технику дифференцирования и интегрирования изучать после того, как проделана эта подготовительная работа, то их можно осваивать одновременно, экономя на этом много времени. И совершенно не нужно давать много сложных интегралов. Хватит нескольких простейших, остальные – если понадобятся – есть в справочниках, теперь – в том числе в электронных. Все это в “том” эксперименте осталось непонятым, невостребованным, никого не вдохновляло, да и не соответствовало духу “министерских контрольных работ”. Потому постепенно все вернулось на круги своя.
А между тем, на самом деле большая часть того, на что тратятся усилия в стремлении “выполнить программу”, никому не нужна. Сошлюсь опять-таки на собственный опыт. За всю последующую учебу и работу мне ни разу не понадобились 90% тех интегралов, которым нас учили. Не сталкивался и с искусственными приемами решения нелинейных дифференциальных уравнений. Когда же пришлось столкнуться с задачами на интегрирование функций и дифференциальных уравнений, то всегда прибегал к помощи справочников. И уж вовсе бесполезной считаю трату времени на задачи по теории пределов (кроме двух “замечательных” пределов), решаемые до изучения правила Лопиталя.
Иногда приходится слышать, что эти задачи (неопределенное интегрирование, вычисление пределов) полезны для тренировки в тождественных преобразованиях. Я на это отвечу: тот, кто не научился этому в школе, здесь ничего нового не приобретет. Старые пробелы заполнять нужно, но на дополнительных занятиях, а не на новом материале. “Не накладывай трудность на трудность!” Зато чего действительно не хватало в моем математическом образовании, так это теории вероятностей, теории случайных процессов, численных методов, теории уравнений в частных производных. Всему этому пришлось учиться самому, многое пришло слишком поздно. Как я потом понял, в заводской исследовательской работе я мог бы принести гораздо больше пользы, если бы владел всем этим с самого начала. И, конечно, еще одной областью – методом структурных схем, но о нем я скажу особо и в своем месте.
Если говорить о главной проблеме в математическом образовании в техническом Вузе вообще, металлургическом в частности – то она в том, чтобы с самого начала показать студенту нужность математики в его специальности, а для этого преподаватель математики должен в общих чертах представлять себе эту будущую специальность и подбирать соответствующие примеры. Выпускающая кафедра должна иметь право голоса при формировании программ и методик по математике.
Принималось множество решений о непрерывной математической подготовке, но вся работа сводилась к составлению формальных отчетов. Мне неизвестен ни один случай, когда госбюджетная работа или диссертация преподавателя математики имела бы отношение к будущей специальности студентов, которых он учит (если не считать такие традиционно математизированные специальности, как автоматика или электротехника – но и тут исследования преследуют вовсе не дидактические цели).
6. О теории функций комплексного переменного. Когда я учился на 4 курсе, в ЛПИ проходили занятия по математике для аспирантов, которые я стал посещать. Курс ТФКП читал профессор Ю.В. Линник (впоследствии очень известный математик). Зачем мне это понадобилось? Я слышал, что ТФКП – мощный теоретический прием, и ожидал проникновения с его помощью в сокровенные тайны природы, что-нибудь на уровне механизма явлений. Этим ожиданиям подсознательно способствовала мистическая тайна мнимой единицы. На деле все оказалось много проще и приземленнее.
Сразу произвело впечатление начало курса. Каждый знает по себе, какой дискомфорт вызывает у начинающего понятие мнимого (и комплексного) числа. Этот дискомфорт проходит постепенно, но не от понимания, а от привыкания. Ю.В. сумел ввести это понятие просто и естественно, без всяких затруднений. Сделал он это настолько красиво, что не могу удержаться от того, чтобы воспроизвести здесь его путь.
Начал он с того, что комплексное число – это плоский, то есть двухкоординатный вектор, а сама ТФКП – хорошее средство упростить решение плоской задачи. Ее разновидности – обтекание воздухом крыла самолета, фильтрация воды через грунт под плотиной, электрическое и магнитное поля вокруг линии электропередачи. Общее в них – то, что вдоль одной из координат ничего не меняется, и можно рассматривать единственное поперечное сечение.
Вектор, идущий в данную точку из начала координат, определяется двумя компонентами – горизонтальной и вертикальной. Чтобы их различать, по горизонтали откладывают обычную единицу, а по вертикали – единицу той же длины, но называемую i – и никаких упоминаний о ее мнимости. Складывают комплексные числа по общим правилам сложения векторов: покомпонентно.
Кроме прямоугольных координат, для описания векторов (и комплексных чисел) используют полярные координаты, задавая длину вектора (модуль) и угол наклона (аргумент), отсчитываемый против часовой стрелки от горизонтальной оси.
Чтобы ввести операцию умножения комплексных чисел, он вначале сформулировал правило умножения обычных чисел в таком виде: произведение C = a · b получается из множимого a тем же путем, каким множитель b получается из единицы. А именно: для получения b единицу растягивают в b раз; для получения c то же проделывают с множимым a – растягивают его в b раз. Логично распространить это правило и на комплексные числа. Но для этого его, естественно, нужно дополнить: ведь чтобы получить b, единицу не только растянули, но и повернули на угол – аргумент множителя. Поступая так же и с множимым, придем к правилу: при умножении комплексных чисел их модули перемножают, а аргументы складывают.
Теперь можно выяснить, чему равно i. Чтобы получить i из единицы, единичный вектор повернули против часовой стрелки на 90 градусов. Чтобы умножить i на i, этот вектор, направленный вверх, нужно еще раз повернуть на 90 градусов, и он окажется направлен влево, то есть, будет равен –1. Отсюда сразу же следует, что i 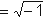 . Это оказывается не исходным пунктом теории, а неизбежным следствием соглашений, принятых для непротиворечивости действий с плоскими векторами, как с обобщением понятия числа. И никаких натяжек, никакой мистики, возникающей при общепринятом порядке изложения! Геометрическую интерпретацию комплексных чисел, как известно, придумал Гаусс еще в 19 веке. Но именно как интерпретацию – после того, как мнимая единица уже введена под этим названием, как
. Это оказывается не исходным пунктом теории, а неизбежным следствием соглашений, принятых для непротиворечивости действий с плоскими векторами, как с обобщением понятия числа. И никаких натяжек, никакой мистики, возникающей при общепринятом порядке изложения! Геометрическую интерпретацию комплексных чисел, как известно, придумал Гаусс еще в 19 веке. Но именно как интерпретацию – после того, как мнимая единица уже введена под этим названием, как 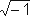 . Линник же начал с векторов, и пришел к тому же корню как к следствию. Кто не видит разницы, тот лишен педагогического чувства.
. Линник же начал с векторов, и пришел к тому же корню как к следствию. Кто не видит разницы, тот лишен педагогического чувства.
Интересно, что за прошедшие с тех пор 50 лет я ни разу не встречал этого вывода ни в учебниках, ни в лекционных курсах. (Сам Линник не писал учебников по ТФКП – это была не его специальность, он занимался другими вопросами). По-прежнему начинают с того, что i 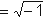 , и что эту величину (неизвестно почему!) принято откладывать на графике по вертикали, правило умножения выводится чисто алгебраически, а геометрия уже вытекает из него, и т.д. Особенно досадно, что исключением не стала и книга Я.Б. Зельдовича и А.Д. Мышкиса “Элементы прикладной математики”.
, и что эту величину (неизвестно почему!) принято откладывать на графике по вертикали, правило умножения выводится чисто алгебраически, а геометрия уже вытекает из него, и т.д. Особенно досадно, что исключением не стала и книга Я.Б. Зельдовича и А.Д. Мышкиса “Элементы прикладной математики”.
Вроде бы то же самое, только в обратном порядке, а в итоге – скучно и неубедительно. Воистину, прав Пушкин: мы ленивы и нелюбопытны! И после этого толкуют о том, что “студенты не хотят учиться”. Да их же старательно отучают от здравого смысла!
Добавление 2000 г. Впоследствии я обнаружил такое же, как у Линника, введение в теорию комплексных чисел в несколько неожиданном месте – в книге Р.В. Поля “Оптика”. Это – очень любопытный факт. Физик, притом в монографии, посвященной специальному разделу этой науки, счел нужным отвлечься на чисто математический вопрос, то есть явно вышел за рамки своей задачи. И вопрос не сегодня возникший, а можно сказать классический, с большой бородой. Ясно, что автор не был удовлетворен его изложением теми, кому это положено по профилю и просто не мог смолчать. И это – ответ тем математикам, которые, случалось, высмеивали меня за то, что я лезу не в свое дело, и пропагандирую подход Линника, в то время, как все это всем “давно известно”. И вот еще интересная мысль. Отец Ю.В. Линника, академик В.А. Линник, был крупным физиком – оптиком, и наверняка был знаком с Р.В. Полем. Думаю, что источник вдохновения тут был общий, хотя и не берусь судить, кто из троих был первооткрывателем. Я вспомнил об этом, разглядывая мемориальную доску на доме напротив БАН – библиотеки Академии Наук на Васильевском острове в СПб, где жил В.А.
А вот и о практическом выходе. Сложные геометрические конфигурации с помощью ТФКП можно преобразовывать в более простые, удобные для расчета, и тем самым этот расчет облегчать. Для этой цели используется аппарат конформных преобразований. Проще всего его представить так. Допустим, у нас есть лист плоской резины, настолько эластичный, что его можно деформировать, не нарушая плоскости – растягивать в одних местах или направлениях и сжимать в других, но так, что любой угол при этом сохраняет свою величину (в этом и состоит конформность). Например, концентрические окружности можно превратить в эксцентричные и обратно; прямые, проходящие через общий центр, при этом превратятся в пучок окружностей, пересекающихся с исходными окружностями под прямыми углами. Кольцевой сектор можно превратить в прямоугольник. Внешнюю и внутреннюю части круга можно поменять местами. Разнообразие здесь очень велико.
Превратив сложную конфигурацию в простую, для нее выполняют расчет, а потом возвращаются к исходной, показав на ней интенсивности тока жидкости, напряженности поля, и т.д. Помню, особое впечатление произвело преобразование Жуковского w=z+1/z, переводящее профиль крыла самолета в окружность. С трудом верилось, что в столь простой формуле спрятано такое глубокое содержание. Был и второй повод для эмоций. О том, что Н.Е. Жуковский – дедушка русской авиации, все мы давно знали. Но что среди инструментов раскрытия авиационных секретов была ТФКП с ее конформными преобразованиями, и что он не просто воспользовался готовым аппаратом, приспособив его к конкретной задаче, а усовершенствовал его, проявив не только инженерное, но и математическое творчество – вот это было откровение. В том же духе – математические достижения кораблестроителя А.Н. Крылова, тоже исходившие из собственных практических нужд. Эти (и другие) примеры свидетельствуют: профессиональные математики далеко не всегда сдают свою продукцию “под ключ”, и инженеры не могут рассчитывать на полный сервис с их стороны.
Очень скоро (при дипломном проектировании) я нашел подходящий объект, чтобы опробовать эту технику и самому. Боковая круглая шахта горения воздухонагревателя расположена таким образом, что ее внутренняя поверхность и наружная стенка кожуха аппарата сильно эксцентричны, и рассчитать тепловые потери через кладку в этой зоне простыми средствами невозможно. Есть примитивный выход – принять по данным практики (читай – “с потолка”) долю потерь, и этим ограничиться. Но в моем проекте была задана необычно высокая температура дутья, и нужно было возможно точнее определить ожидаемую температуру горения и другие параметры. Я решил применить конформное преобразование, чтобы с его помощью превратить эксцентричные окружности в концентричные. Выглядит оно совсем несложно: W = (Z-Z1) / (Z-Z2). Здесь z1 и z2 – точки пересечения двух вспомогательных окружностей, ограничивающих обсчитываемый сектор, которые на новом поле превращаются в лучи. Точка z1 превращается в новый общий центр, а z2 уходит в бесконечность. Стенка превратилась в цилиндрическую, расчет для которой затруднений не вызывает. (На самом деле он оказался чуть сложнее, чем описано, из-за того, что кладка была трехслойной: динас, шамот и теплоизоляционный кирпич, и окружностей получилось четыре, а строго концентричными можно было сделать только две. Но здесь эксцентриситет был уже мал, и я обошелся некоторым огрублением, подробности опускаю).
Расчет вызвал неудовольствие рецензента – заведующего доменным сектором ЛенГипромеза. Он сделал замечание: зачем так усложнять задачу? Ему было невдомек, что задача не усложняется, а упрощается, а без этого приема для той конфигурации вообще неразрешима на уровне знаний, предусмотренных программой. С помощью уравнения теплопроводности и используя ЭВМ, ее можно решить, но процедура эта весьма громоздка. С помощью же ТФКП она элементарно решается без всяких ЭВМ (их в то время никто из нас и в глаза не видел). Для человека, не знакомого с ТФКП, это, конечно, усложнение. Эмпирический (потолочный) коэффициент рецензента вполне бы устроил.
7. Из преподавательской практики. В курсе ТМП (ФХМП) пришлось рассказывать о сравнительно новом способе контроля и описания характеристик пористой структуры руды, кокса и других материалов. Измеряется распределение поверхности пор по их радиусам. Для этого применяют специальные графики – программы в двух вариантах: дифференциальные и интегральные. Нужно уметь их читать и переходить от одного к другому. Эта операция сильно затрудняла студентов, из-за чего и весь раздел считался очень трудным. Между тем, в точности такую процедуру они уже проделывали до того по меньшей мере трижды. Первый раз – изучая соотношение между производной и интегралом в курсе математики. Второй раз – строя эпюры перерезывающей силы и изгибающего момента для прямой балки в курсе сопромата. Третий раз – сопоставляя графики плотности и функции распределения случайной величины в теории вероятностей. И вот, столкнувшись с задачей в четвертый раз, они находились в таком же тупике, как в трех предыдущих.
Добавление 2000 г. На самом деле не четвертый, а по меньшей мере девятый. Ведь были еще скорость и пройденный путь, сила и работа, и т.д.
Добавление 2003 г. Теперь я составил таблицу из 20 строк аналогичного содержания, но и она не полная.
А ведь достаточно было по-настоящему понять ее при первом с ней столкновении, и каждый следующий раз навык ее решения все более закреплялся бы. Разумеется, я все это им говорил и упрекал в том, что они не ценят собственного времени. Вместо того, чтобы хорошо разобрать вопрос один раз, они мучились над ним четыре раза – и все впустую. Хотя на самом деле я понимал, что гораздо больше, чем студенты, виноваты преподаватели и авторы учебников по математике. Читая этот материал в первый раз, математик должен был дать им практические навыки пользования простейшими графиками (чего не заменяют самые головоломные задачи на дифференцирование и интегрирование), и предупредить о том, где и сколько раз им придется с этим столкнуться. Но... снова см. у Пушкина!
А ведь именно здесь резерв тех самых часов, которых так не хватает при их дележе между “фундаменталами” и “прикладниками”. Нужен взаимный интерес и взаимодействие, а не взаимные упреки. То же и с физикой.
От редакции ПРЕТИЧ. Эти материалы мне выслал сам их Автор еще в 2007-2008 годах, он называл все это "пока еще черновики". Лично я не был с ним знаком, только по переписке через интернет. Я думал, что эти материалы были навсегда утеряны, но нашел компакт диски, на которые делал резервные копии с жесткого диска. Было большим трудом восстановить с них информацию! Но кое-что ценное это мне принесло. В том числе и эти материалы.
***
 Такой раздел может показаться странным при моей профессии. Но большинство моих металлургических забот, так или иначе, были связаны с математикой, особенно после появления ЭВМ, когда реальностью стали математические модели металлургических процессов. Приходилось многое осваивать самому – вузовского багажа не хватало: составители учебных программ считали, что металлургам математика не особо нужна.
Такой раздел может показаться странным при моей профессии. Но большинство моих металлургических забот, так или иначе, были связаны с математикой, особенно после появления ЭВМ, когда реальностью стали математические модели металлургических процессов. Приходилось многое осваивать самому – вузовского багажа не хватало: составители учебных программ считали, что металлургам математика не особо нужна.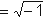 . Это оказывается не исходным пунктом теории, а неизбежным следствием соглашений, принятых для непротиворечивости действий с плоскими векторами, как с обобщением понятия числа. И никаких натяжек, никакой мистики, возникающей при общепринятом порядке изложения! Геометрическую интерпретацию комплексных чисел, как известно, придумал Гаусс еще в 19 веке. Но именно как интерпретацию – после того, как мнимая единица уже введена под этим названием, как
. Это оказывается не исходным пунктом теории, а неизбежным следствием соглашений, принятых для непротиворечивости действий с плоскими векторами, как с обобщением понятия числа. И никаких натяжек, никакой мистики, возникающей при общепринятом порядке изложения! Геометрическую интерпретацию комплексных чисел, как известно, придумал Гаусс еще в 19 веке. Но именно как интерпретацию – после того, как мнимая единица уже введена под этим названием, как 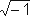 . Линник же начал с векторов, и пришел к тому же корню как к следствию. Кто не видит разницы, тот лишен педагогического чувства.
. Линник же начал с векторов, и пришел к тому же корню как к следствию. Кто не видит разницы, тот лишен педагогического чувства.